آيا دوست داريد با ذهنتان شوخي كنيد؟ اگر موافق هستيد به سوالات زير پاسخ دهيد .اين كار نه تنها براي روحتان مناسب است، بلكه خستگي تان را نيز بر طرف مي كند . از جواب دادن به اين سوالات لذت ببريد و پاسخهايتان را با جوابهاي داده شده مقايسه كنيد...
جذر به معنی ریشه ، بن و پایه است. در ریاضیات جذر گرفتن عکس عمل به توان رساندن می باشد.
سوال هوش؟!
خرسی از نقطه p یک کیلومتر به سمت جنوب حرکت میکند، سپس یک کیلومتر به سمت شرق میرود و در انتها یک کیلومتر به سمت شمال میرود و به نقطه p میرسد!! ( برای دقت بیشتر توصیه میکنم حتما" شکل رسم کنید.) حال سوال این است که رنگ خرس چیست؟
همه ما میدانیم که خرس یا سفید است یا قهوه ای ویا خرس پاندا است. پس ، لطفا جواب های خود و راه رسیدن به جوابرا در قسمت "نظر بدهید" ویا " ؟ نظر " بیان نمائید.
این سوال در کتاب چگونه مسئله حل کنیم تالیف جرج پولیا آمده است.
به 12 تا چوب کبریت چند تا مربع ( هم اندازه ) می توان ساخت ؟
( نمی توانید چوب ها بشکنید )
جواب هایتان را در قسمت نظرات بیان کنید.
مختصات(سال دوم راهنمایی)
دو محور عمود بر هم که در یک صفحه قرار دارند ، یک دستگاه مختصات به وجود می آورند.
محور افقی را محور طول، محور عمودی را ...
ادامه مطلب
کوچکترین مضرب مشترک: (ک.م.م)
نشان میدهیم.
برای هر عدد صحیح a مخالف صفر وجود ندارد زیرا مضارب صفر خود صفر است پس مجموعه مضارب مثبت آن تهی است پس ک.م.م aو0 وجود ندارد. قضیه: ک.م.م دو عدد صحیح ناصفر a و b حتما وجود دارد.
حتما وجود دارد بنابراین مجموعه مضارب مشترک a و b یعنی S را در نظر میگیریم : 
و چون به وضوح S زیر مجموعه ای از اعداد طبیعی است بر طبق اصل خوشترتیبی می توان گفت S دارای عضو مینیمم است یعنی کوچکترین عضوی در S چون m وجود دارد که: 
مثال: 
را بیابید:
پاسخ:
1- مجموعه مضارب مثبت 8= 
2- مجموعه مضارب مثبت 10=
مشاهده می شود کوچکترین عضو مشترک از مجموعه مضارب مشترک 8 و 10 برایر 40 است پس
.
تاریخچه اعداد اول
بعد از دوران یونان باستان، نظریه اعداد در سده شانزدهم و هفدهم با زحمات ویت دو مزیریاک ، دوباره مورد توجه قرار گرفت. در قرن هجدهم اویلر و لاگرانژ به قضیه پرداختند و در همین مواقع لوژاندرو گاوس به آن تعبیر علمی بخشیدند. در ۱۸۰۱ گاوس در مقاله Disquisitiones Arithmeticæ حساب نظریه اعداد مدرن را پایه گذاری کرد.
چبیشف کران هایی برای تعداد اعداد اول بین یک بازه ارائه داد. ریمان اظهار کرد که حد تعداد اعداد اول از یک عدد داده شده تجاوز نمیکند. (قضیه عدد اول) و آنالیز مختلط را در تئوری تابع زتای ریمان گنجاند. و فرمول صریح تئوری اعداد اول را از صفرهای آن نتیجه گرفت. تئوری همنهشتی از گاوس شروع شد. او علامتگذاری زیر را پیشنهاد کرد:
چبیشف در سال ۱۸۴۷ به زبان روسی کاری را در این زمینه منتشر کرد و سره آن را در فرانسه عمومی کرد. بجای خلاصه کردن کارهای قبلی، لوژاندر قانون تقابل درجهٔ دوم را گذاشت. این قانون از استقراء کشف شد و قبلاً اویلر آن را مطرح کرده بود. لوژاندر در کتاب تئوری اعداد برای حالتهای خاص آن را ثابت کرد. جدا از کارهای اویلر و لوژاندر، گاوس این قانون را در سال ۱۷۹۵ کشف کرد و اولین کسی بود که یک اثبات کلی ارائه داد. کوشی ؛ دیریشله او یک مقاله کلاسیک است؛ جکوبی که علامت جکوبی را معرفی کرد؛ لیوویل ؛ زلر ؛ آیزنشتین ؛ کومر و کرونکر نیز در این زمینه کارهایی کردهاند. این تئوری تقابل درجه دوم و سوم را شامل میشود (گاوس؛ جکوبی که اولین بار قانون تقابل درجه سوم را ثابت کرد ؛ و کومر).
نمایش اعداد با صورت درجه دوم ...
ادامه مطلب
عدد پی از عددهای ثابت ریاضی و تقریباً برابر با ۳٫۱۴۱۵۹ است. این عدد را با علامت π نشان میدهند. عدد پی عددی حقیقی و گُنگ است که نسبت محیط دایره به قطر آن را در هندسهٔ اقلیدسی مشخص میکند و کاربردهای فراوانی در ریاضیات، فیزیک و مهندسی دارد. عدد پی همچنین به ثابت ارشمیدس نیز معروف است.
در قرن نهم هجری دانشمند وریاضی دان ایرانی غیاثالدین جمشید کاشانی عدد پی راتا شانزده رقم اعشار محاسبه کرده بود به نحوی که تا صد و پنجاه سال بعد کسی نتوانست آن را گسترش دهد: ۲π=۶٫۲۸۳۱۸۵۳۰۷۱۷۹۵۸۶۵
|
|
عدد پی عدد گنگی است که در بسیاری از محاسبات ریاضی به نحوی حضور دارد و از مهمترین اعداد کاربردی در ریاضیات میباشد. آن را با π نمایش میدهند. در هندسه اقلیدسی دو بعدی، این عدد را نسبت محیط دایره به قطر دایره و یا مساحت دایرهای به شعاع واحد تعریف میکنند. در ریاضیات مدرن این عدد را در آنالیز ریاضی و با استفاده از توابع مثلثاتی، به صورت دقیق ریاضی تعریف میکنند. به عنوان نمونه عدد پی را دو برابر کوچکترین مقدار مثبت x، که به ازای آن cos(x) = 0 میشود تعریف میکنند.
 |
| اعداد رومی |
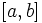اعداد به عنوان پایه و اساس علم ریاضیات ، در زندگی روزمره نیز نقشی غیر قابل انکار دارند درباره عدد و تاریخچه اختراع آن سخن بسیار می توان گفت ، در این مطلب سعی شده گزیده مختصری از تاریخچه اعداد رومی ارائه گردد :
در روش مصریها برای ساختن عددها، به عدد « ده » به خاطر وجود ده انگشت در دو دست، اهمیت فراوان داده می شد.
مایانها (Mayans)، مردمی که در قسمت ...
ادامه مطلب
تاریخچه پیدایش عدد و شمارش
جذر :
جذر به معنی ریشه ، بن و پایه است. در ریاضیات جذر گرفتن عکس عمل به توان رساندن می باشد.
ادامه مطلب
اگه تو نستی این سوال حل کنی ؟